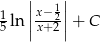Zadanie nr 2362892
Oblicz całkę 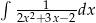 .
.
Rozwiązanie
Rozkładamy mianownik na czynniki
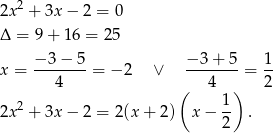
Funkcja podcałkowa jest więc sumą dwóch ułamków prostych pierwszego rodzaju
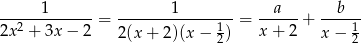
Mnożymy obie strony przez 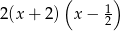 .
.
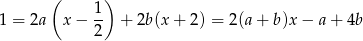
Mamy stąd układ równań.
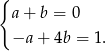
Dodając równania stronami mamy 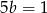 , czyli
, czyli 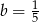 . Stąd
. Stąd 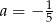 , oraz
, oraz
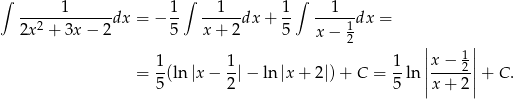
Odpowiedź: