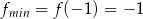Zadanie nr 2429416
Wyznacz wartość największą i najmniejszą funkcji 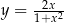 w przedziale
w przedziale 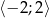 .
.
Rozwiązanie
Liczymy pochodną
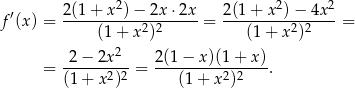
Widać zatem, że na przedziałach 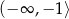 i
i 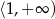 funkcja maleje (pochodna jest ujemna), a na przedziale
funkcja maleje (pochodna jest ujemna), a na przedziale 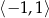 rośnie (pochodna dodatnia). Zatem w
rośnie (pochodna dodatnia). Zatem w 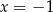 jest minimum lokalne, a w
jest minimum lokalne, a w 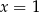 maksimum lokalne. Możemy sobie schematycznie naszkicować wykres funkcji
maksimum lokalne. Możemy sobie schematycznie naszkicować wykres funkcji 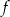 .
.
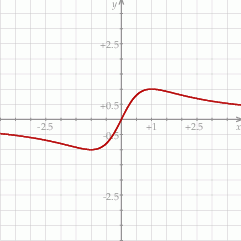
Wartość największa będzie przyjęta w maksimum lokalnym lub w lewym końcu przedziału (bo przy prawym funkcja maleje). Sprawdzamy
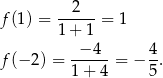
Zatem 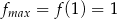 .
.
Wartość najmniejsza będzie przyjęta w minimum lokalnym lub w prawym końcu przedziału (bo przy lewym funkcja maleje). Sprawdzamy
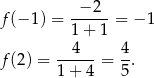
Zatem 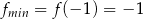 .
.
Odpowiedź: 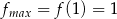 oraz
oraz