Zadanie nr 2485070
Oblicz objętość bryły otrzymanej w wyniku obrotu wokół osi 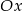 trapezu krzywoliniowego ograniczonego przez wykres funkcji
trapezu krzywoliniowego ograniczonego przez wykres funkcji 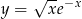 , proste
, proste 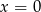 i
i 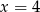 oraz oś
oraz oś 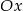 .
.
Rozwiązanie
Najpierw obrazek.
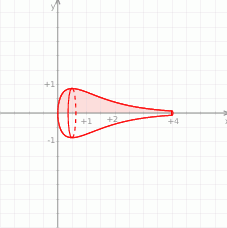
Korzystamy ze wzoru
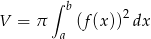
na objętość bryły otrzymanej przez obrót wokół osi 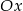 obszaru zwartego pod wykresem funkcji
obszaru zwartego pod wykresem funkcji 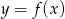 , gdzie
, gdzie ![x ∈ [a,b]](https://img.zadania.info/zad/2485070/HzadR4x.gif) .
.
Liczymy
![| | ∫ 4 −2x |u = x v ′ = e− 2x | V = π xe dx = ||u′ = 1 v = − 1e−2x|| = [ 0 ] 2 [ ] 1 − 2x 4 π ∫ 4 −2x − 8 π 1 −2x 4 = π − -xe + -- e dx = − 2πe + -- − --e = 2 0 2 0 2 2 0 −8 π- − 8 π- π- 9π- −8 = − 2πe − 4e + 4 = 4 − 4 e .](https://img.zadania.info/zad/2485070/HzadR5x.gif)
Odpowiedź: