Cała zabawa z przekształcaniem wykresów funkcji sprowadza się do następującego pytania: w jaki sposób zmieni się wzór funkcji jeżeli dokonamy przekształcenia jej wykresu? Oczywiście odpowiedź zależy od tego, jakie przekształcenie mamy na myśli. Przesuwanie wykresów Jest prosta zależność między przesunięciem wykresu funkcji, a zmianą jej wzoru. Zanim jednak przejdziemy do szczegółów wyjaśnijmy, że przesunięcie wykresu o 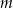 jednostek wzdłuż osi oznacza przesunięcie wykresu o
jednostek wzdłuż osi oznacza przesunięcie wykresu o  jednostek w kierunku strzałki na osi jeżeli
jednostek w kierunku strzałki na osi jeżeli  , oraz o
, oraz o 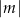 jednostek w przeciwnym kierunku jeżeli
jednostek w przeciwnym kierunku jeżeli 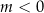 .
.
Przesunięcie wykresu funkcji o 2 jednostki wzdłuż osi 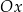 i o
i o 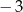 jednostki wzdłuż osi
jednostki wzdłuż osi  oznacza przesunięcie wykresu o 2 jednostki w prawo i o 3 w dół.
oznacza przesunięcie wykresu o 2 jednostki w prawo i o 3 w dół.
Żeby się nie pogubić, osobno przedstawimy każdą z trzech możliwych konfiguracji.
1. Przesunięcie wykresu o 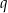 jednostek wzdłuż osi
jednostek wzdłuż osi 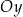 . Jest to zdecydowanie najprostsza sytuacja: wzór funkcji
. Jest to zdecydowanie najprostsza sytuacja: wzór funkcji 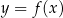 po przesunięciu będzie miał postać
po przesunięciu będzie miał postać
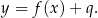
Mam nadzieję, że nie budzi to wątpliwości: dodanie do wzoru funkcji liczby 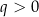 sprawia, że każda wartość funkcji jest większa o
sprawia, że każda wartość funkcji jest większa o 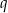 , czyli wykres przesuwa się o
, czyli wykres przesuwa się o 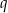 jednostek do góry. Jeżeli natomiast
jednostek do góry. Jeżeli natomiast 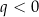 to wartości się zmniejszają, czyli przesuwamy w dół.
to wartości się zmniejszają, czyli przesuwamy w dół.
Pierwszy wykres przedstawia parabolę  , a drugi parabolę
, a drugi parabolę  .
.
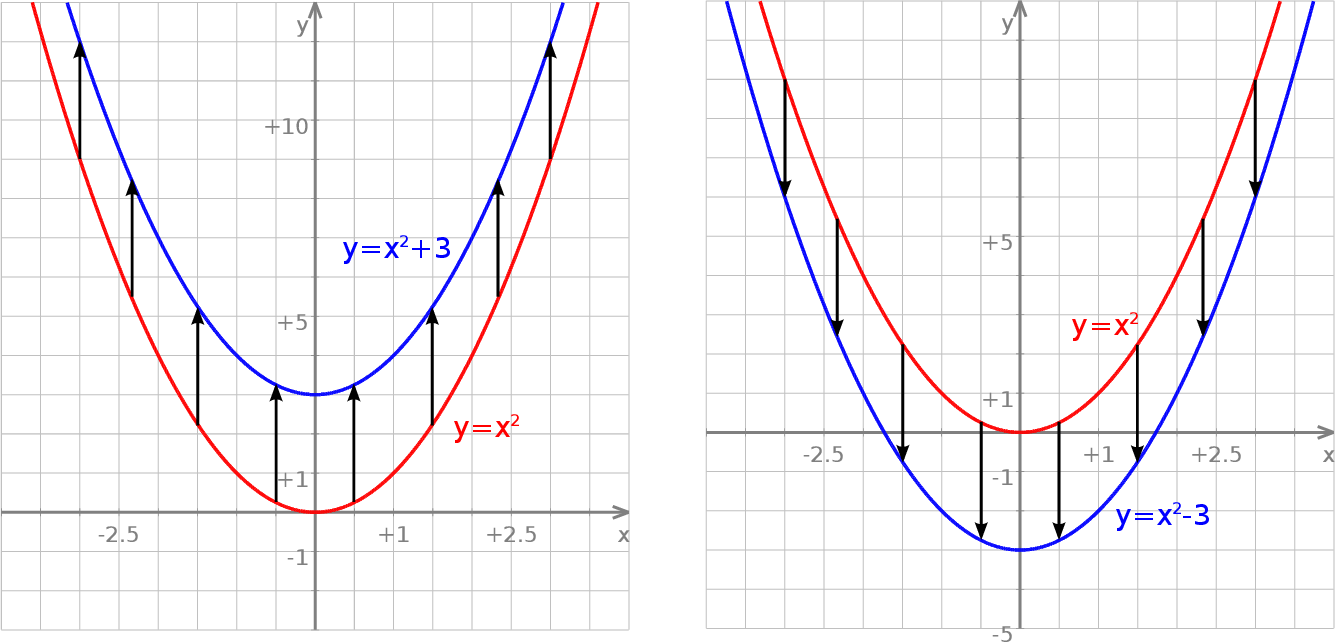
Obie parabole powstają przez przesunięcie paraboli 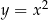 o 3 jednostki: pierwsza do góry, a druga w dół.
o 3 jednostki: pierwsza do góry, a druga w dół.
2. Przesunięcie wykresu o 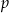 jednostek wzdłuż osi
jednostek wzdłuż osi 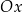 . Tym razem wzór funkcji
. Tym razem wzór funkcji 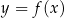 po przesunięciu będzie miał postać
po przesunięciu będzie miał postać
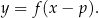
Wyjaśnijmy krótko skąd wziął się minus w nawiasie.
Zastanówmy się jak narysować wykres funkcji 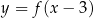 . W punkcie
. W punkcie 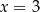 mamy wartość
mamy wartość 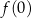 , w punkcie
, w punkcie 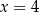 mamy wartość
mamy wartość 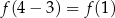 , itd.: w punkcie
, itd.: w punkcie  zaznaczamy wartość
zaznaczamy wartość 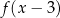 . To oznacza, że wszystkie wartości funkcji
. To oznacza, że wszystkie wartości funkcji 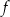 , czyli cały wykres, zostały przesunięte o 3 jednostki w prawo. Oczywiście myślimy analogicznie, gdy zamiast 3 jest
, czyli cały wykres, zostały przesunięte o 3 jednostki w prawo. Oczywiście myślimy analogicznie, gdy zamiast 3 jest 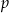 .
.
Pierwszy wykres przedstawia parabolę 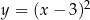 , a drugi parabolę
, a drugi parabolę 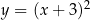 .
.
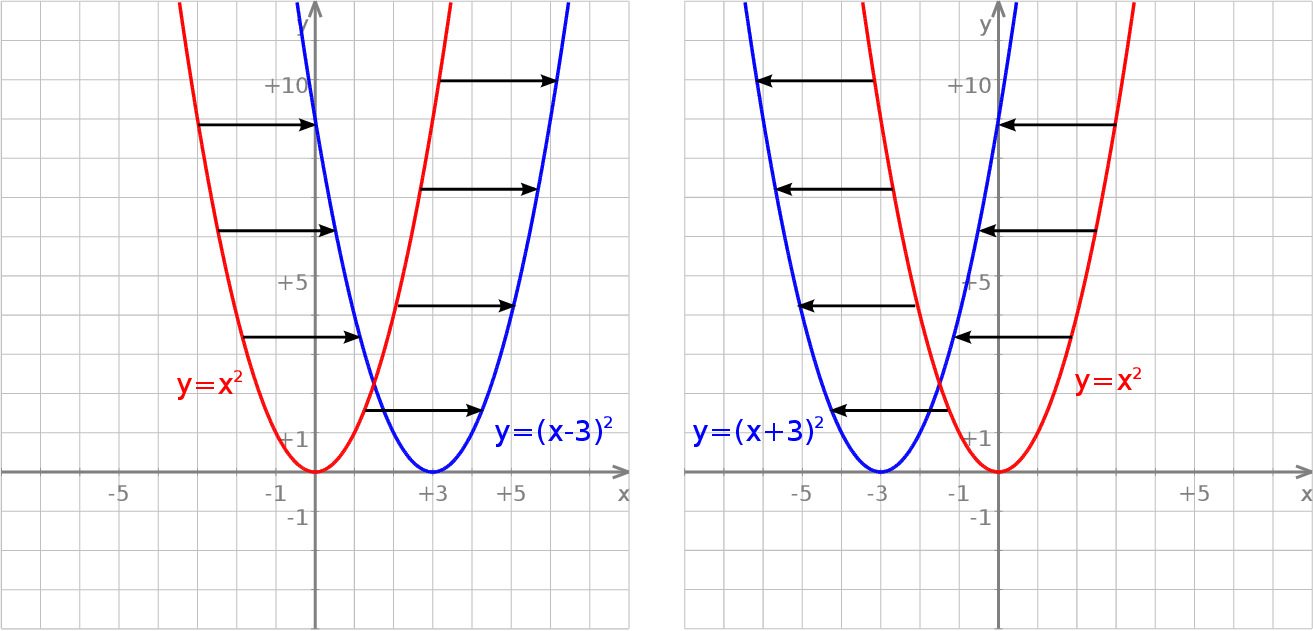
Obie parabole powstają przez przesunięcie paraboli 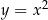 o 3 jednostki: pierwsza do prawo, a druga w lewo.
o 3 jednostki: pierwsza do prawo, a druga w lewo.
3. Przesunięcie wykresu o wektor ![[p,q]](https://img.zadania.info/por/0028578/HporT37x.png) . W zasadzie jest to połączenie dwóch poprzednich sytuacji: przesunięcie wykresu o wektor
. W zasadzie jest to połączenie dwóch poprzednich sytuacji: przesunięcie wykresu o wektor ![[p,q ]](https://img.zadania.info/por/0028578/HporT38x.png) to dokładnie to samo, co jednoczesne przesunięcie o
to dokładnie to samo, co jednoczesne przesunięcie o 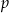 jednostek wzdłuż osi
jednostek wzdłuż osi 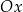 i
i 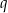 jednostek wzdłuż osi
jednostek wzdłuż osi 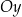 . Mamy więc wzór przesuniętej funkcji:
. Mamy więc wzór przesuniętej funkcji:
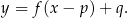
Pierwszy wykres przedstawia parabolę 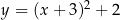 , a drugi parabolę
, a drugi parabolę 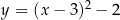 .
.
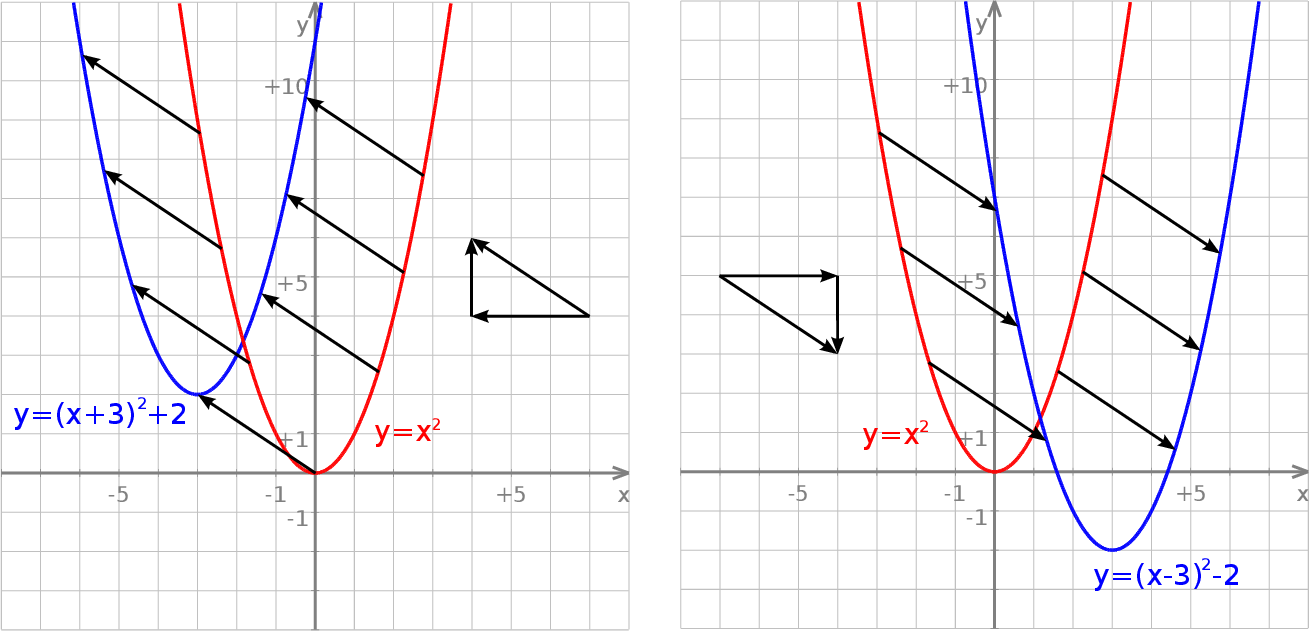
Obie parabole powstają przez przesunięcie paraboli  : pierwsza o wektor
: pierwsza o wektor ![[− 3,2 ]](https://img.zadania.info/por/0028578/HporT48x.png) , a druga o wektor
, a druga o wektor ![[3 ,−2 ]](https://img.zadania.info/por/0028578/HporT49x.png) .
.
Odbicia wykresów Rozpocznijmy od najprostszej sytuacji.
Wykres funkcji 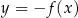 powstaje z wykresu
powstaje z wykresu 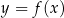 przez odbicie względem osi
przez odbicie względem osi 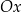 .
.
Podobnie jest odbiciem względem osi 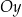 .
.
Wykres funkcji 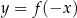 powstaje z wykresu
powstaje z wykresu 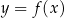 przez odbicie względem osi
przez odbicie względem osi 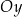 .
.
Mam nadzieje, że powyższe wzory wydają się wam dość oczywiste, jeżeli jednak tak nie jest, to spróbujcie pomyśleć w jaki sposób narysować wykresy funkcji 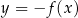 i
i 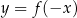 , jeżeli umiecie liczyć wartości funkcji
, jeżeli umiecie liczyć wartości funkcji 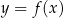 (czyli znacie jej wykres).
(czyli znacie jej wykres).
Pierwszy wykres przedstawia funkcję 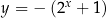 , a drugi
, a drugi
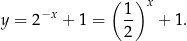
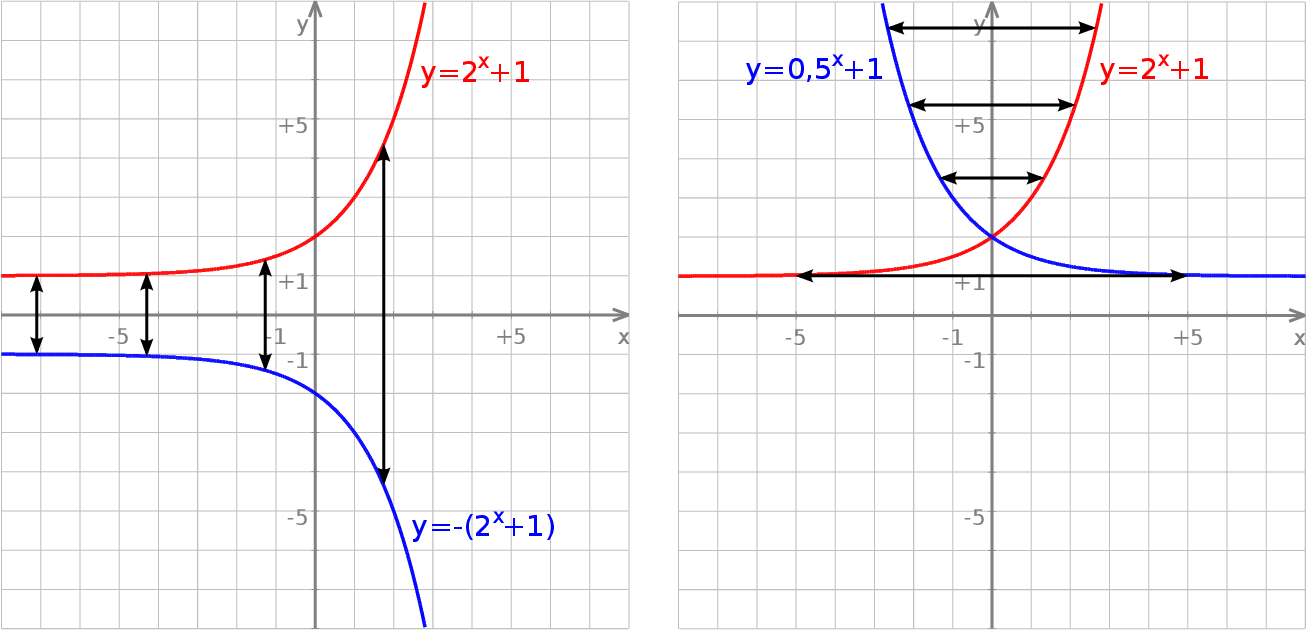
Oba wykresy powstają przez odbicie wykresu funkcji 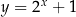 : pierwszy względem osi
: pierwszy względem osi 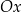 , a drugi względem osi
, a drugi względem osi 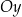 .
.
Jeżeli wykonamy oba powyższe odbicia na raz, to otrzymamy symetrię względem początku układu współrzędnych.
Wykres funkcji 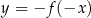 powstaje z wykresu
powstaje z wykresu 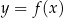 przez symetrię względem punktu
przez symetrię względem punktu 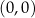 .
.
Na lewym obrazku narysowany jest wykres funkcji 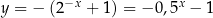 , który powstaje z wykresu funkcji
, który powstaje z wykresu funkcji 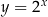 przez symetrię względem początku układu współrzędnych.
przez symetrię względem początku układu współrzędnych.
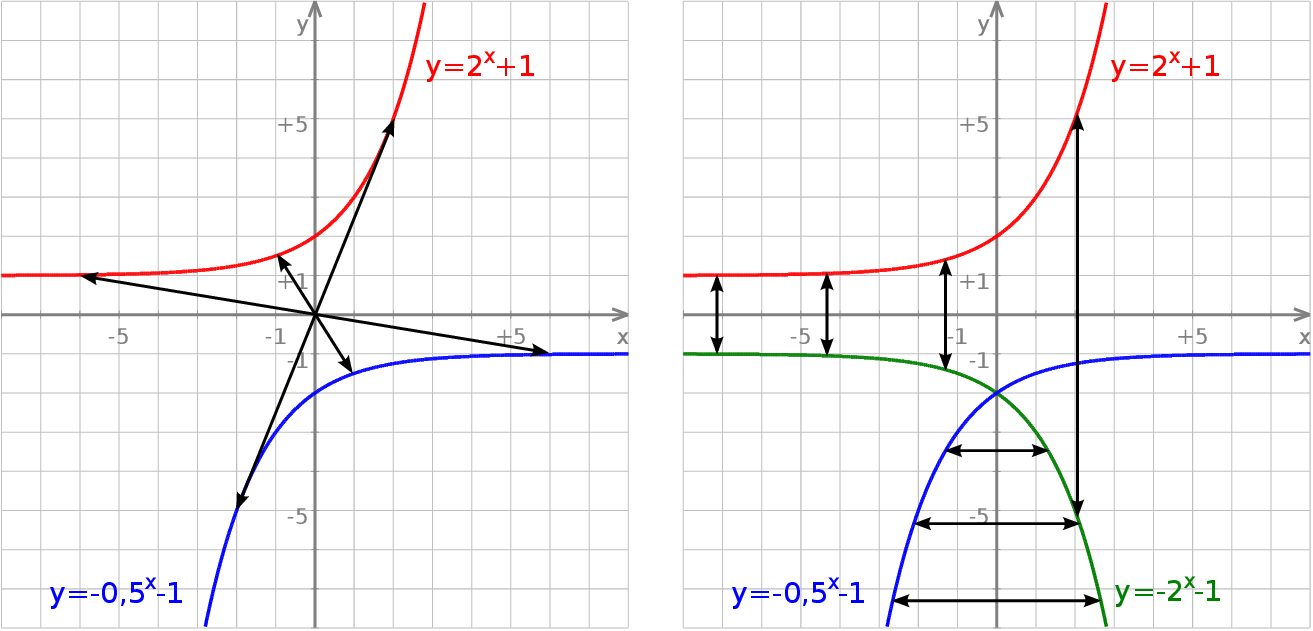
Prawy obrazek pokazuje, że symetria względem początku układu współrzędnych to dokładnie to samo, co wykonanie odbicia względem osi 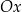 , a potem względem osi
, a potem względem osi 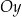 (kolejność tych odbić nie ma znaczenia).
(kolejność tych odbić nie ma znaczenia).
Złożenia z wartością bezwzględną Jak zwykle zaczynamy od najprostszej sytuacji.
Wykres funkcji 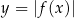 powstaje z wykresu
powstaje z wykresu 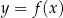 przez odbicie części znajdującej poniżej osi
przez odbicie części znajdującej poniżej osi 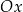 do góry.
do góry.
Powyższe sformułowanie jest dość niezręczne, ale powinno być jasne, o co chodzi: punkty wykresu, które są powyżej osi 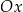 pozostają na swoim miejscu, a punkty, które są poniżej osi
pozostają na swoim miejscu, a punkty, które są poniżej osi 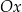 , odbijamy względem tej osi (czyli wędrują do góry).
, odbijamy względem tej osi (czyli wędrują do góry).
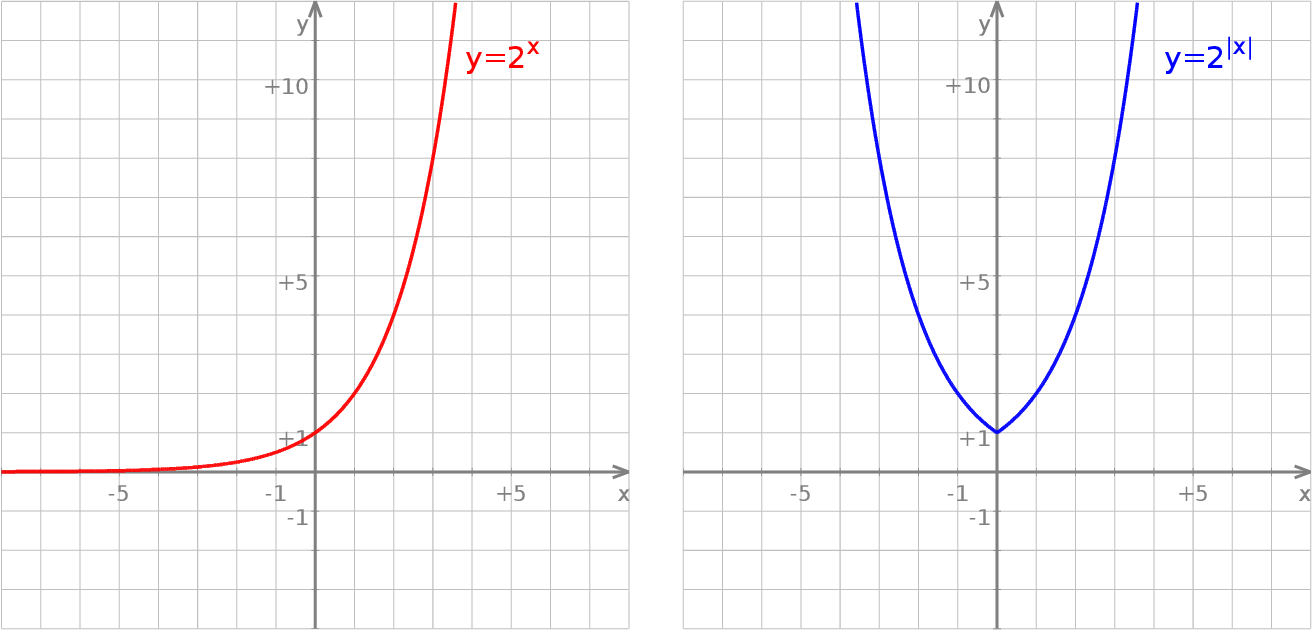
Jeżeli natomiast wstawimy wartość bezwzględną do środka funkcji 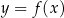 , czyli zajmujemy się funkcją postaci
, czyli zajmujemy się funkcją postaci 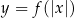 to sytuacja jest odrobinę ciekawsza. Zauważmy, że jeżeli
to sytuacja jest odrobinę ciekawsza. Zauważmy, że jeżeli 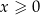 to nowo otrzymana funkcja niczym się nie różni od funkcji
to nowo otrzymana funkcja niczym się nie różni od funkcji 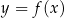 (bo wtedy
(bo wtedy 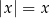 ), czyli na prawo od osi
), czyli na prawo od osi 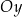 wykresy obydwu funkcji będą identyczne. Jeżeli natomiast
wykresy obydwu funkcji będą identyczne. Jeżeli natomiast 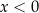 to mamy
to mamy 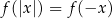 , czyli wykres na lewo od osi
, czyli wykres na lewo od osi 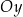 powstaje przez odbicie prawej części wykresu
powstaje przez odbicie prawej części wykresu 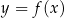 względem tej osi.
względem tej osi.
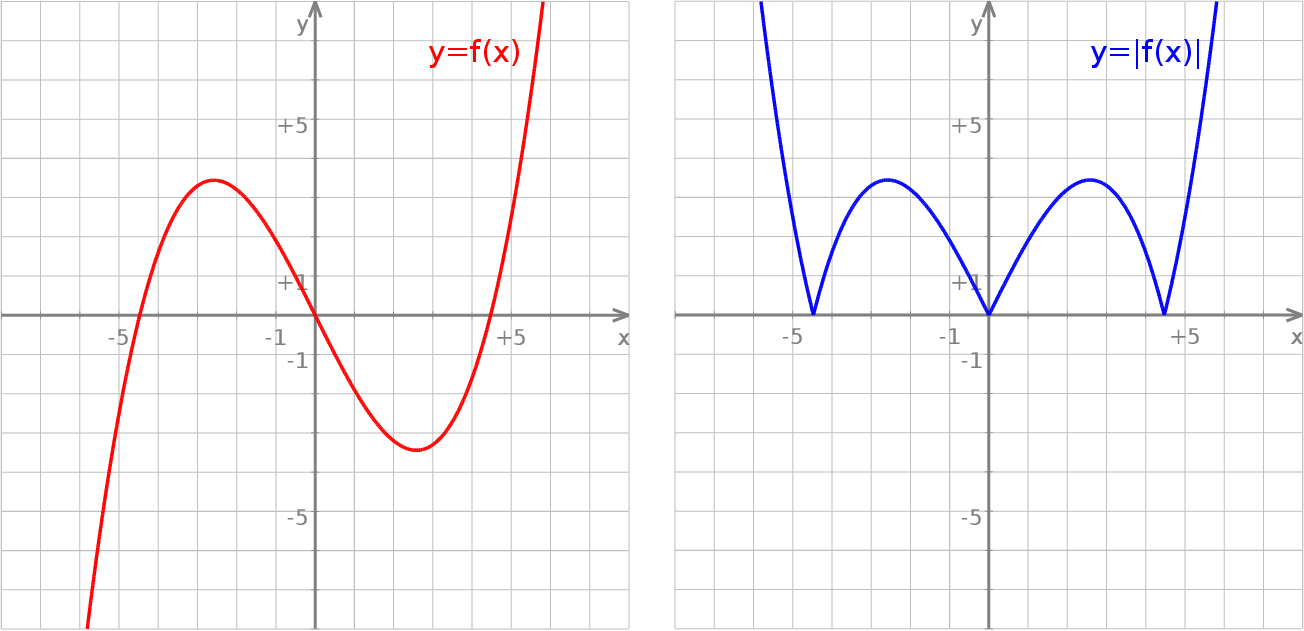
Wykres funkcji 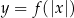 powstaje z wykresu
powstaje z wykresu 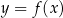 przez pozostawienie fragmentu wykresu na prawo od osi
przez pozostawienie fragmentu wykresu na prawo od osi 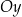 bez zmian, oraz przez odbicie tej części wykresu względem osi
bez zmian, oraz przez odbicie tej części wykresu względem osi 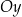 .
.

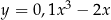 oraz funkcji
oraz funkcji 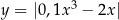 .
.
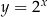 oraz funkcji
oraz funkcji 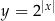 .
.