Zadanie nr 2868948
Oblicz całkę 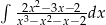 .
.
Rozwiązanie
Rozłóżmy licznik i mianownik na czynniki.
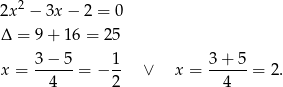
Zatem
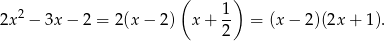
Teraz rozkładamy mianownik. Sprawdzając dzielniki wyrazu wolnego, można znaleźć pierwiastek 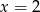 . Zatem mianownik dzieli się przez
. Zatem mianownik dzieli się przez 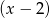 . Dzielimy
. Dzielimy
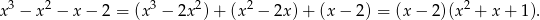
Mamy zatem
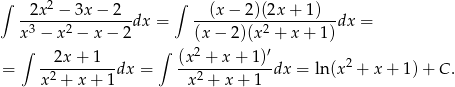
Odpowiedź: