Agitacja Korzystając ze wzoru na sumę początkowych wyrazów ciągu geometrycznego łatwo wyprowadzić wzór
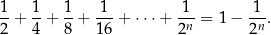
Oczywiście liczba 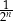 dla dużych
dla dużych  jest mikroskopijnie mała, więc można powiedzieć, że powyższa suma „zbliża” się do 1 dowolnie blisko. Mówiąc dokładniej, jeżeli będziemy zwiększać
jest mikroskopijnie mała, więc można powiedzieć, że powyższa suma „zbliża” się do 1 dowolnie blisko. Mówiąc dokładniej, jeżeli będziemy zwiększać  to suma będzie coraz mniej różnić się od 1. Zupełnie formalnie takie rzeczy zapisuje się za pomocą granic, ale na użytek szkolny używa się zapisu
to suma będzie coraz mniej różnić się od 1. Zupełnie formalnie takie rzeczy zapisuje się za pomocą granic, ale na użytek szkolny używa się zapisu
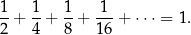
Celowo z lewej strony nie napisaliśmy ostatniego składnika sumy, bo zapis ten ma sugerować, że dodajemy do siebie wszystkie wyrazy ciągu (a więc dodajemy do siebie nieskończenie wiele liczb). Sens tego dodawania, jak i wyniku z prawej strony wyjaśniliśmy wyżej: dodając do siebie liczby z lewej strony zbliżamy się do 1, im więcej liczb do siebie dodamy, tym bliżej znajdziemy się 1.
Od razu zauważmy, że dodawanie do siebie nieskończenie wielu liczb nie zawsze ma sens.
Suma
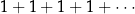
nie dąży do żadnej liczby – dodając jedynki z lewej strony możemy otrzymać dowolnie dużą liczbę. Symbolicznie zapisujemy to wzorem
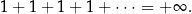
Jeszcze gorzej jest z sumą
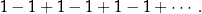
Dodając po kolei składniki z lewej strony na przemian mamy 1 i 0. Trudno w takiej sytuacji sensownie zdefiniować wynik takiego dodawania.
Definicje Opisaną wyżej operację dodawania do siebie nieskończenie wielu liczb nazywa się w matematyce szeregiem liczbowym. Jeżeli dodatkowo liczby, które do siebie dodajemy są kolejnymi wyrazami ciągu geometrycznego, to mówimy o szeregu geometrycznym.
Ze wzoru na  -ty wyraz ciągu geometrycznego wiemy, że każdy szereg geometryczny ma postać
-ty wyraz ciągu geometrycznego wiemy, że każdy szereg geometryczny ma postać
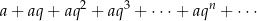
Mówimy, że szereg jest zbieżny jeżeli jego suma jest liczbą (w takim samym sensie jak w pierwszym przykładzie tego poradnika). Jeżeli szereg nie jest zbieżny to mówimy, że jest on rozbieżny.
Szereg geometryczny
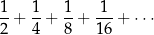
jest zbieżny do liczby 1.
Szeregi geometryczne
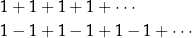
są rozbieżne.
Wzór Widzieliśmy wyżej, że niektóre szeregi geometryczne są zbieżne (czyli ich suma ma sens), a inne nie. Okazuje się, że jest bardzo prosta charakteryzacja, kiedy szereg geometryczny jest zbieżny.
Niezerowy szereg geometryczny
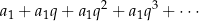
jest zbieżny wtedy i tylko wtedy, gdy 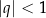 .
.
Co więcej, mamy bardzo prosty wzór na sumę szeregu
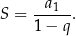
Na mocy powyższego wzoru mamy
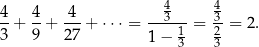
Szereg geometryczny
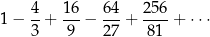
jest rozbieżny, bo 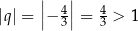 .
.
W kwadrat o boku 1 wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Obliczmy sumę pól wszystkich tych kwadratów.

Jeżeli oznaczmy bok jednego z kwadratów przez  , to okrąg wpisany w ten kwadrat ma średnicę
, to okrąg wpisany w ten kwadrat ma średnicę  . Jednocześnie jest to przekątna kolejnego kwadratu, czyli jego bok ma długość
. Jednocześnie jest to przekątna kolejnego kwadratu, czyli jego bok ma długość 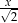 . Zatem pole kolejnego kwadratu jest dwa razy mniejsze od pola poprzedniego kwadratu. Pierwszy kwadrat ma pole 1, więc szukana suma jest równa
. Zatem pole kolejnego kwadratu jest dwa razy mniejsze od pola poprzedniego kwadratu. Pierwszy kwadrat ma pole 1, więc szukana suma jest równa
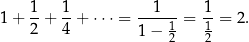
Równania i nierówności Popularny motyw zadań szkolnych to równania i nierówności, w których jedna ze stron jest sumą szeregu geometrycznego. W tego typu zadaniach mamy do wykonania trzy czynności.
-
Po pierwsze wyznaczamy dziedzinę danego równania/nierówności. Oprócz standardowych mianowników, pierwiastków, logarytmów etc., sprawdzamy kiedy dany szereg geometryczny jest zbieżny – sprowadza się to do rozwiązania nierówności
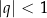 .
. -
Zastępujemy dany szereg geometryczny jego sumą, zgodnie ze wzorem
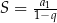 .
. -
Rozwiązujemy otrzymane równanie/nierówność (w którym nie ma już żadnych kropek) i odrzucamy rozwiązania, które nie są zawarte w wyznaczonej wcześniej dziedzinie.
Rozwiążmy równanie: 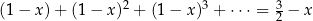 .
.
Z lewej strony równania mamy szereg geometryczny o ilorazie 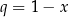 , sprawdźmy kiedy jest on zbieżny
, sprawdźmy kiedy jest on zbieżny
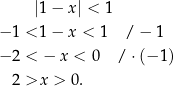
Teraz rozwiązujemy równanie
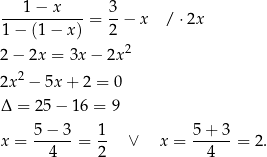
Drugie rozwiązanie odrzucamy, bo nie należy do dziedziny równania.

