Zadanie nr 3185623
Zbadaj monotoniczność ciągu danego wzorem 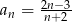 .
.
Rozwiązanie
Aby sprawdzić monotoniczność ciągu musimy sprawdzić, czy różnica 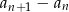 jest stale dodatnia (ciąg rosnący), czy też stale ujemna (ciąg malejący).
jest stale dodatnia (ciąg rosnący), czy też stale ujemna (ciąg malejący).
Liczymy różnicę kolejnych wyrazów
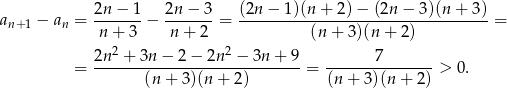
Zatem ciąg jest rosnący.
Odpowiedź: Ciąg jest rosnący

