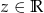Zadanie nr 3194550
Znaleźć rozwiązanie układu równań 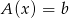 , dla:
, dla:
![[1 2 − 3] [ 2 ] A = , b = 2 1 − 2 − 1](https://img.zadania.info/zad/3194550/HzadT1x.gif)
Rozwiązanie
Będziemy rozwiązywać układy zapisując je w macierzy – dzięki temu nie będziemy musieli pisać niewiadomych (które i tak nie są do niczego potrzebne). Będziemy dążyć do uzyskania kolumn z jedną niezerową liczbą i samymi zerami (będziemy je oznaczać na niebiesko). Taka kolumna oznacza, że odpowiadająca jej niewiadoma występuje tylko w jednym równaniu i możemy ją z tego równania wyliczyć w zależności od pozostałych niewiadomych. Gdy już nie da się tej operacji kontynuować (ilość niebieskich kolumn jest równa ilości równań) to pozostałe niewiadome traktujemy jak parametry. Ważne jest, aby przekształcenia wykonywać tylko na wierszach.
Jeżeli ktoś nie przyzwyczajony do rozwiązywania układów równań w macierzy to może sobie równolegle pisać cały układ równań – w ten sposób łatwo docenić metodę macierzową (jest dużo mniej pisania).
Liczymy
![[ | ] [ | ] [ | ] 1 2 −3 |2 1 2 − 3 | 2 1 0 − 1 |− 4 2 1 −2 |−1 = 0 − 3 4 |− 5 = 0 − 3 43 |− 35 { | W2− 2W 1 | W1+ 23W2 | x = 1z− 4 3 3 − 3y = −4z − 5 ⇒ y = 43z + 53.](https://img.zadania.info/zad/3194550/HzadR0x.gif)
Zatem wszystkie rozwiązania są postaci
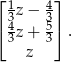
Odpowiedź: 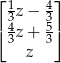 gdzie
gdzie