Zadanie nr 3616815
Zbadać, czy podany ciąg jest ograniczony z dołu i czy jest ograniczony z góry 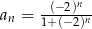 .
.
Rozwiązanie
Jeżeli  jest parzyste to mamy
jest parzyste to mamy
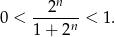
Jeżeli natomiast  jest nieparzyste, to mamy
jest nieparzyste, to mamy
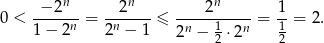
Odpowiedź: Ciąg jest ograniczony.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Zbadać, czy podany ciąg jest ograniczony z dołu i czy jest ograniczony z góry 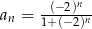 .
.
Jeżeli  jest parzyste to mamy
jest parzyste to mamy
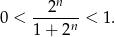
Jeżeli natomiast  jest nieparzyste, to mamy
jest nieparzyste, to mamy
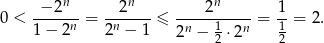
Odpowiedź: Ciąg jest ograniczony.
