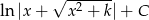Zadanie nr 3876353
Oblicz całkę 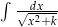 .
.
Rozwiązanie
Sposób I
Stosujemy I podstawienie Eulera 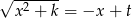 . Mamy wtedy
. Mamy wtedy
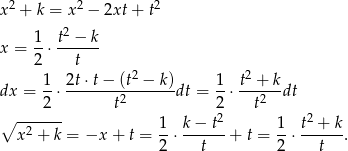
Stąd
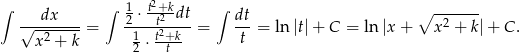
Sposób II
Jeżeli nie boimy się funkcji hiperbolicznych, to szukaną całkę możemy łatwo obliczyć podstawiając 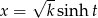 lub
lub 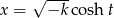 (w zależności od znaku
(w zależności od znaku 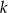 ). Będziemy korzystać z wzorków
). Będziemy korzystać z wzorków
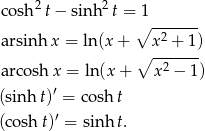
Jeżeli 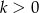 to podstawiamy
to podstawiamy 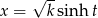 . Mamy wtedy
. Mamy wtedy
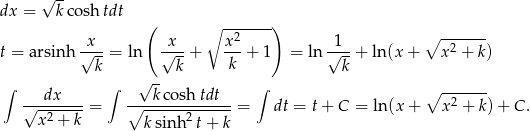
Jeżeli natomiast 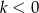 i
i 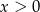 to podstawiamy
to podstawiamy 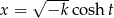 . Mamy wtedy
. Mamy wtedy
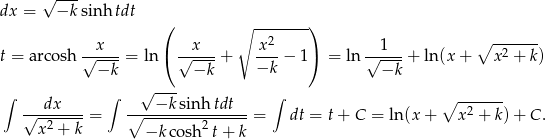
Tak naprawdę pozostał jeszcze przypadek 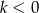 i
i 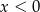 . Można wtedy podstawić
. Można wtedy podstawić 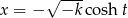 i śledząc powyższy rachunek otrzymamy
i śledząc powyższy rachunek otrzymamy
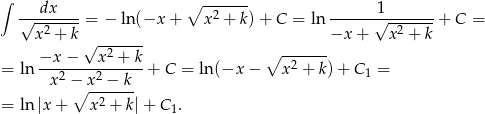
Widać więc, że to dokładnie na użytek tego przypadku jest wartość bezwzględna we wzorze
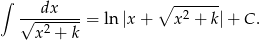
Odpowiedź: