Zadanie nr 4111497
Znaleźć funkcję odwrotną do funkcji: 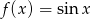 dla
dla ![π-3π- x ∈ [2; 2 ]](https://img.zadania.info/zad/4111497/HzadT1x.gif) .
.
Rozwiązanie
Funkcją odwrotną do funkcji 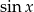 jest funkcja
jest funkcja 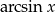 . Problem polega jednak na tym, że definiując
. Problem polega jednak na tym, że definiując 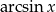 obcinamy sinusa do przedziału
obcinamy sinusa do przedziału ![[− π2, π2]](https://img.zadania.info/zad/4111497/HzadR3x.gif) , a tu mamy inny przedział. Aby sobie z tym poradzić, musimy przesunąć argument sinusa o
, a tu mamy inny przedział. Aby sobie z tym poradzić, musimy przesunąć argument sinusa o 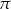 w lewo. Robi się to następująco:
w lewo. Robi się to następująco:
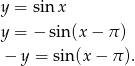
Teraz argumenty sinusa z prawej strony są dokładnie z takiego przedziału o jaki nam chodzi, czyli możemy do obu stron przyłożyć 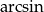 .
.
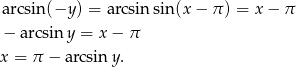
Na koniec możemy zamienić literki, żeby  był argumentem, a
był argumentem, a 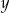 wartością.
wartością.
Odpowiedź: