Zadanie nr 4123820
Wyznaczyć wszystkie macierze stopnia 2, których kwadrat jest równy macierzy ![[ ] 2 0 0 2](https://img.zadania.info/zad/4123820/HzadT0x.gif) .
.
Rozwiązanie
Mamy równanie
![[ ]2 [ ] a b = 2 0 c d 0 2 [a2 + bc ab + bd] [2 0] 2 = ac+ cd bc + d 0 2 ( a2 + bc = 2 |||{ b(a+ d) = 0 | c(a+ d) = 0 ||( 2 bc+ d = 2.](https://img.zadania.info/zad/4123820/HzadR0x.gif)
Ze środkowych równań wynika, że 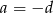 lub
lub 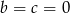 . W tej drugiej sytuacji dostajemy układ
. W tej drugiej sytuacji dostajemy układ
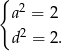
Daje to nam cztery rozwiązania
![[ √ -- ] [ √ -- ] [ √ -- ] [ √ -- ] 2 √0--, − 2 √0--, 2 0√ --, − 2 0√ -- 0 2 0 2 0 − 2 0 − 2](https://img.zadania.info/zad/4123820/HzadR4x.gif)
Zajmijmy się teraz przypadkiem 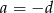 . Z układu pozostaje nam wtedy równanie
. Z układu pozostaje nam wtedy równanie
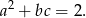
Jeżeli 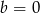 lub
lub 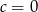 to mamy
to mamy 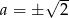 i
i  lub
lub 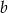 dowolne. Można o tych rozwiązaniach myśleć jak o uogólnieniu otrzymanych wcześniej.
dowolne. Można o tych rozwiązaniach myśleć jak o uogólnieniu otrzymanych wcześniej.
Jeżeli 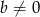 i
i 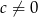 , to
, to 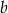 wybieramy dowolnie,
wybieramy dowolnie,  też dowolnie i mamy
też dowolnie i mamy
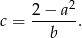
Daje to nam macierze postaci
![[ ] a b 2−a2 −a b](https://img.zadania.info/zad/4123820/HzadR17x.gif)

