Zadanie nr 4254559
Zbadaj zbieżność ciągu 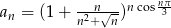 .
.
Rozwiązanie
Podane wyrażenie powinno się kojarzyć z granicą typu  do czegoś. Ponieważ jednak jest cosinus, który może być czasem dodatni, a czasem ujemny, granica ta raczej nie powinna istnieć. Spróbujemy to uzasadnić.
do czegoś. Ponieważ jednak jest cosinus, który może być czasem dodatni, a czasem ujemny, granica ta raczej nie powinna istnieć. Spróbujemy to uzasadnić.
Musimy wskazać dwa podciągi, które mają różne granice. Jeżeli weźmiemy  postaci
postaci 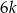 to
to
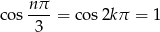
i mamy
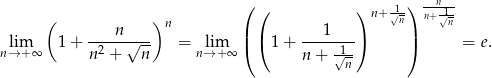
Podobnie, dla 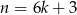 dostajemy
dostajemy
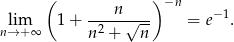
Odpowiedź: Ciąg jest rozbieżny

