Zadanie nr 4780962
Wyznacz wartość największą i najmniejszą funkcji 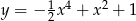 w przedziale
w przedziale 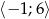 .
.
Rozwiązanie
Sposób I
Jest to funkcja dwukwadratowa, więc podstawiamy 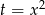 , ze względu na przedział zmienności
, ze względu na przedział zmienności  ,
, 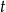 zmienia się w przedziale
zmienia się w przedziale 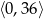 . Szukamy zatem wartości paraboli
. Szukamy zatem wartości paraboli
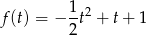
w przedziale 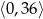 . Wierzchołek tej paraboli jest w punkcie
. Wierzchołek tej paraboli jest w punkcie
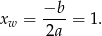
Zatem w tym punkcie jest przyjmowana wartość największa
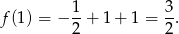
Wartość najmniejsza jest przyjmowana w jednym z końców przedziału, sprawdźmy w którym.
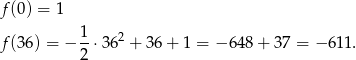
Sposób II
Zadanie możemy też rozwiązać pochodnymi.
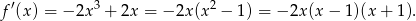
Widać zatem, że funkcja rośnie na przedziałach 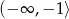 i
i 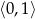 (pochodna dodatnia) oraz maleje na przedziałąch
(pochodna dodatnia) oraz maleje na przedziałąch 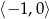 i
i 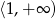 (pochodna jest ujemna). Żeby się nie pogubić wygodnie naszkicować sobie schematyczny wykres funkcji
(pochodna jest ujemna). Żeby się nie pogubić wygodnie naszkicować sobie schematyczny wykres funkcji  .
.
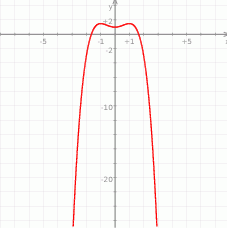
Są zatem dwa maksima lokalne w 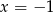 i
i 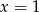 oraz minimum lokalane w
oraz minimum lokalane w 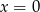 . Największa wartość jest w jednym z maksimów. Liczymy
. Największa wartość jest w jednym z maksimów. Liczymy
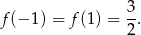
Najmniejsza wartość będzie na końcu przedziału lub w minimum
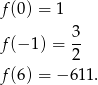
Odpowiedź: 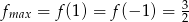 oraz
oraz