Zadanie nr 4955152
Oblicz całkę 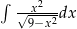 .
.
Rozwiązanie
Sposób I
Stosujemy metodę współczynników nieoznaczonych, czyli szukamy stałych 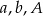 takich, że
takich, że
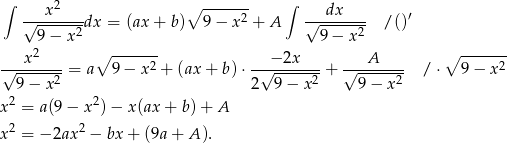
Mamy stąd 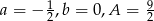 . Zatem
. Zatem
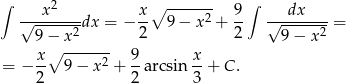
Skorzystaliśmy wyżej ze wzoru
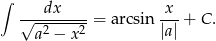
Sposób II
Podstawiamy 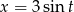 , gdzie
, gdzie ![t ∈ [− π-, π-] 2 2](https://img.zadania.info/zad/4955152/HzadR6x.gif) . Mamy wtedy
. Mamy wtedy
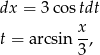
oraz
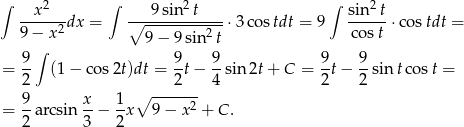
Odpowiedź: