Zadanie nr 5009596
Oblicz całkę 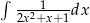 .
.
Rozwiązanie
Sposób I
Zwiniemy mianownik do pełnego kwadratu (postać kanoniczna) i skorzystamy ze wzoru
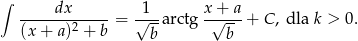
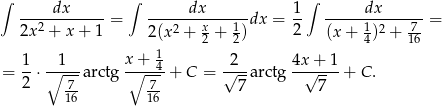
Sposób II
Całkę mogliśmy też policzyć wprost.
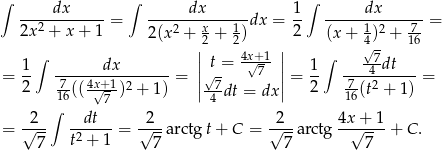
Odpowiedź: 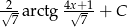
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 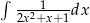 .
.
Sposób I
Zwiniemy mianownik do pełnego kwadratu (postać kanoniczna) i skorzystamy ze wzoru
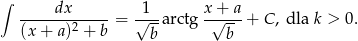
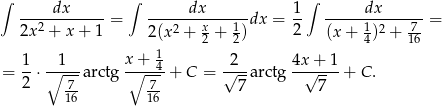
Sposób II
Całkę mogliśmy też policzyć wprost.
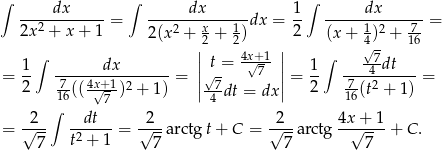
Odpowiedź: