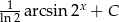Zadanie nr 5098707
Oblicz całkę 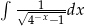 .
.
Rozwiązanie
Przekształćmy najpierw wyrażenie podcałkowe.
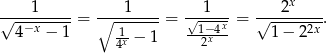
Możemy zatem podstawić 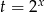 .
.
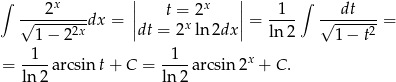
Odpowiedź: 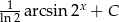
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 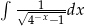 .
.
Przekształćmy najpierw wyrażenie podcałkowe.
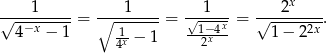
Możemy zatem podstawić 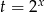 .
.
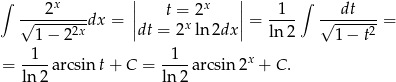
Odpowiedź: