Zadanie nr 5324900
Dany jest ciąg o wyrazie ogólnym 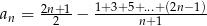 . Zbadaj monotoniczność tego ciągu i oblicz jego granicę.
. Zbadaj monotoniczność tego ciągu i oblicz jego granicę.
Rozwiązanie
Ze wzoru na sumę wyrazów ciągu arytmetycznego mamy
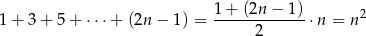
(wyrazów jest  , bo wzór
, bo wzór 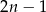 daje nam 1 dla
daje nam 1 dla 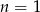 i
i 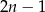 dla
dla  ). Mamy zatem
). Mamy zatem
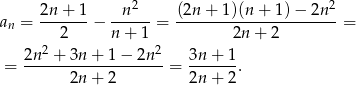
Aby sprawdzić czy ciąg jest monotoniczny, policzmy różnicę jego dwóch kolejnych wyrazów.
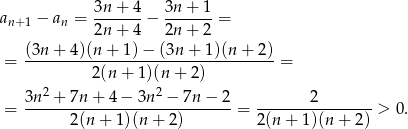
Tak więc ciąg jest rosnący. Policzmy teraz jego granicę.
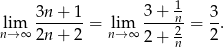
Odpowiedź: Rosnący, granica: 

