Zadanie nr 5390249
Oblicz granicę ciągu 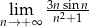 .
.
Rozwiązanie
Gdyby nie było sinusa, to ciąg byłby zbieżny do 0. Sinus niewiele zmienia, bo jest ograniczony. Porządnie możemy to zapisać używając 3 ciągów.
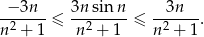
Skrajne ciągi zbiegają do 0, więc środkowy też.
Odpowiedź: 0

