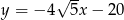Zadanie nr 5698236
Wyznacz wszystkie proste, które są jednocześnie styczne do paraboli 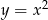 oraz okręgu o równaniu
oraz okręgu o równaniu 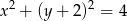 .
.
Rozwiązanie
Szkicujemy opisaną sytuację
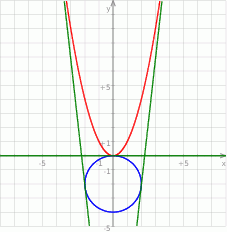
Wyznaczmy najpierw ogólną postać stycznej do danej paraboli w punkcie 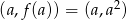 . Liczymy pochodną
. Liczymy pochodną
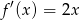
styczna do paraboli w punkcie 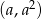 ma więc współczynnik kierunkowy równy
ma więc współczynnik kierunkowy równy 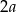 , czyli jest postaci
, czyli jest postaci
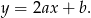
Współczynnik 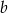 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 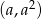 .
.
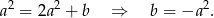
Styczna ma więc postać 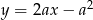 . Jeżeli styczna ta ma być styczna do danego okręgu o środku
. Jeżeli styczna ta ma być styczna do danego okręgu o środku 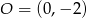 i promieniu
i promieniu 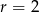 , to środek okręgu
, to środek okręgu 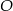 musi być odległy od tej prostej o
musi być odległy od tej prostej o 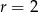 . Korzystamy ze wzoru na odległość punktu
. Korzystamy ze wzoru na odległość punktu 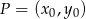 od prostej
od prostej 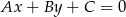 :
:
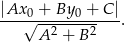
W naszej sytuacji mamy więc równanie
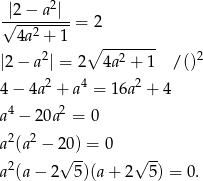
Otrzymujemy stąd trzy proste, które są jednocześnie styczne do danej paraboli i okręgu.
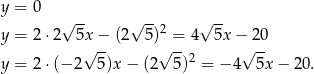
Odpowiedź: 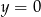 ,
, 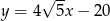 ,
,