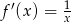Zadanie nr 5750869
Oblicz z definicji pochodną funkcji 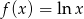 .
.
Rozwiązanie
Będziemy korzystać z granic
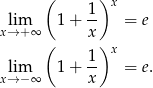
Z tych granic wynika, że
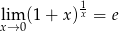
(wystarczy podstawić 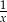 zamiast
zamiast  ). Będziemy też korzystać z ciągłości logarytmu.
). Będziemy też korzystać z ciągłości logarytmu.
Liczymy pochodną w punkcie 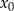 .
.
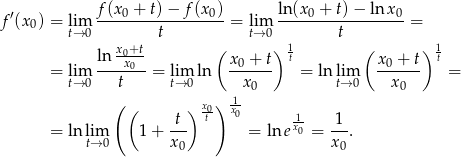
Odpowiedź: