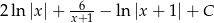Zadanie nr 5855758
Oblicz całkę 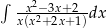 .
.
Rozwiązanie
Szukamy rozkładu funkcji podcałkowej na ułamki proste postaci:
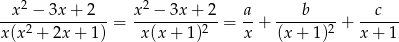
Mnożąc obie strony przez 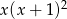 otrzymujemy.
otrzymujemy.
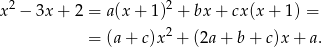
Stąd 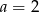 oraz
oraz 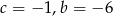 oraz
oraz
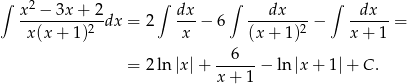
Odpowiedź: 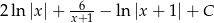
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 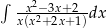 .
.
Szukamy rozkładu funkcji podcałkowej na ułamki proste postaci:
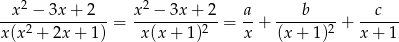
Mnożąc obie strony przez 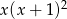 otrzymujemy.
otrzymujemy.
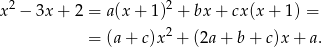
Stąd 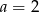 oraz
oraz 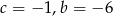 oraz
oraz
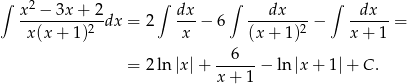
Odpowiedź: