Zadanie nr 6080527
Wykazać, że funkcja 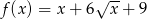 jest różnowartościowa. Wyznaczyć funkcję odwrotną.
jest różnowartościowa. Wyznaczyć funkcję odwrotną.
Rozwiązanie
Zauważmy, że dziedziną podanej funkcji jest zbiór 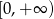 . Wyznaczymy wzór funkcji odwrotnej, co jednocześnie będzie dowodem różnowartościowości funkcji (dla każdego
. Wyznaczymy wzór funkcji odwrotnej, co jednocześnie będzie dowodem różnowartościowości funkcji (dla każdego 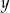 -ka wyznaczymy dokładnie jednego
-ka wyznaczymy dokładnie jednego  -a).
-a).
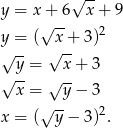
Na koniec możemy zmienić literki tak, aby  było argumentem, z
było argumentem, z 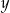 wartością
wartością
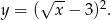
Odpowiedź: