Zadanie nr 6206611
Oblicz całkę 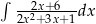 .
.
Rozwiązanie
Rozkładamy mianownik na czynniki
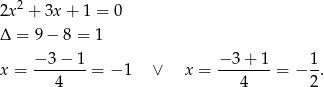
Szukamy zatem rozkładu funkcji podcałkowej na ułamki proste postaci:
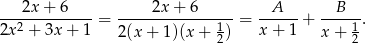
Mnożąc obie strony przez 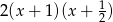 mamy
mamy
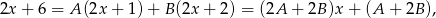
co daje układ równań
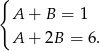
Odejmując od drugiego równania pierwsze otrzymujemy 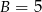 . Stąd
. Stąd 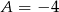 oraz
oraz
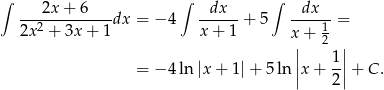
Odpowiedź: