Zadanie nr 6215593
Wykazać, że funkcja przyporządkowująca wielomianowi 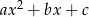 wektor
wektor 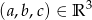 jest izomorfizmem przestrzeni
jest izomorfizmem przestrzeni ![R [x]2](https://img.zadania.info/zad/6215593/HzadT2x.gif) wielomianów stopnia
wielomianów stopnia 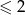 i przestrzeni
i przestrzeni 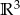 .
.
Rozwiązanie
Sprawdzamy czy podane odwzorowanie 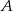 jest liniowe, niech
jest liniowe, niech 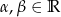 i
i 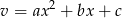 ,
, 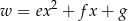 . Wtedy
. Wtedy
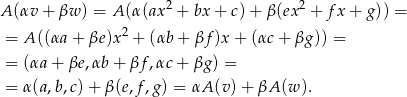
Aby wykazać, że odwzorowanie jest odwracalne, wystarczy zauważyć, że ma trywialne jądro lub że jest „na”. Każda z tych rzeczy jest oczywista.

