Zadanie nr 6746746
Czy zbiór 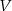 jest podprzestrzenią liniową przestrzeni
jest podprzestrzenią liniową przestrzeni 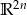 ? Jeśli tak to znaleźć jej bazę.
? Jeśli tak to znaleźć jej bazę.
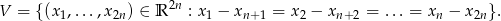
Rozwiązanie
Przede wszystkim zauważmy, że podany warunek oznacza, że współrzędne 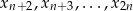 są jednoznacznie wyznaczone przez współrzędne
są jednoznacznie wyznaczone przez współrzędne 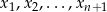 . Rzeczywiście, jeżeli oznaczymy
. Rzeczywiście, jeżeli oznaczymy 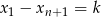 to
to
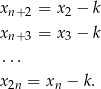
Współrzędne 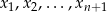 są natomiast zupełnie dowolne.
są natomiast zupełnie dowolne.
Sposób I
Musimy się zastanowić, czy podany zbiór 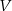 jest zamknięty ze względu sumę i mnożenie przez skalar. Aby nie mieć dwóch warunków, będziemy sprawdzać, czy
jest zamknięty ze względu sumę i mnożenie przez skalar. Aby nie mieć dwóch warunków, będziemy sprawdzać, czy
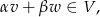
gdzie 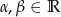 i
i 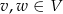 .
.
Jeżeli
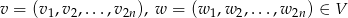
to
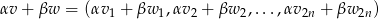
i wektor ten spełnia dany warunek, bo równość
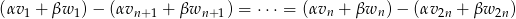
możemy zapisać w postaci
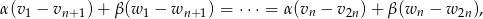
co oznacza, że jest ona konsekwencją założenia 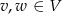 .
.
Przy wyznaczaniu bazy będziemy korzystać z bazy standardowej:
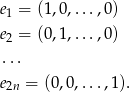
Bazą tej podprzestrzeni jest układ (należy myśleć, że 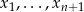 są dowolne, a pozostałe współrzędne są wyznaczone z podanego warunku.)
są dowolne, a pozostałe współrzędne są wyznaczone z podanego warunku.)
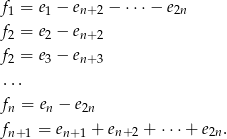
Sprawdźmy, że układ ten jest liniowo niezależny
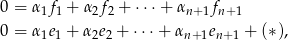
gdzie (*) jest pewną kombinacją wektorów 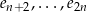 – można ją dokładnie wyliczyć, ale nie ma ona znaczenia (ważne jest tylko, że nie ma tam wektorów
– można ją dokładnie wyliczyć, ale nie ma ona znaczenia (ważne jest tylko, że nie ma tam wektorów 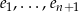 ). Z liniowej niezależności wektorów
). Z liniowej niezależności wektorów 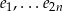 mamy
mamy
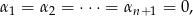
co dowodzi liniowej niezależności wektorów 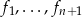 . Pozostało sprawdzić, że generują one
. Pozostało sprawdzić, że generują one 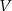 . Dla dowolnego
. Dla dowolnego
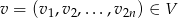
mamy
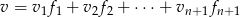
(to wynika z tego, co już napisaliśmy: współrzędne 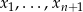 jednoznacznie wyznaczają pozostałe).
jednoznacznie wyznaczają pozostałe).
Sposób II
Tym razem skorzystamy z faktu, że jądro odwzorowania liniowego jest podprzestrzenią liniową. W ten sposób łatwo możemy pokazywać, że zbiory wektorów tworzą podprzestrzenie.
Takie podejście ma jeszcze jedną zaletę, bo ze wzoru
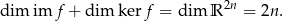
będziemy wiedzieć jaki jest wymiar przestrzeni  . W wszystkich poniższych przykładach
. W wszystkich poniższych przykładach 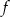 będzie ’na’, więc
będzie ’na’, więc
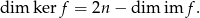
Dzięki temu znajdując bazę nie musimy sprawdzać, czy jej wektory są liniowo niezależne – wystarczy tylko, żeby generowały 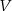 i żeby była ich odpowiednia ilość.
i żeby była ich odpowiednia ilość.
Rozpatrzmy odwzorowanie liniowe
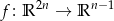
dane wzorem
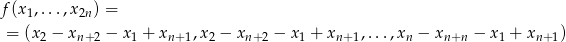
Jego jądro to dokładnie wektory spełniające warunek
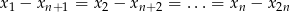
Bazę wyznaczamy jak w poprzednim sposobie, ale nie musimy już wykazywać jej liniowej niezależności.
Sposób III
Jeszcze inny sposób to skorzystanie z ogólnego faktu, że rozwiązania jednorodnego układu równań tworzą podprzestrzeń liniową. Używając tej metody można również wyznaczyć wektory bazowe jako rozwiązania podstawowe odpowiedniego układu równań.

