Zadanie nr 6748954
Oblicz całkę 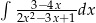 .
.
Rozwiązanie
Funkcja podcałkowa jest sumą dwóch ułamków prostych pierwszego rodzaju, bo mianownik ma dwa pierwiastki rzeczywiste (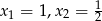 ). Jednak zamiast rozkładać tą funkcję na ułamki proste, lepiej jest zauważyć, że licznik jest równy pochodnej mianownika pomnożonej przez -1. Zatem najprościej jest całkować przez podstawienie.
). Jednak zamiast rozkładać tą funkcję na ułamki proste, lepiej jest zauważyć, że licznik jest równy pochodnej mianownika pomnożonej przez -1. Zatem najprościej jest całkować przez podstawienie.
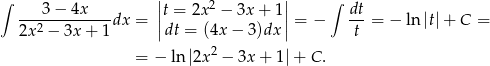
Odpowiedź: