Zadanie nr 7137042
Zbadaj wypukłość funkcji 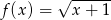 .
.
Rozwiązanie
Ze względu na wyrażenie pod pierwiastkiem musi być 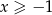 . Liczymy drugą pochodną.
. Liczymy drugą pochodną.
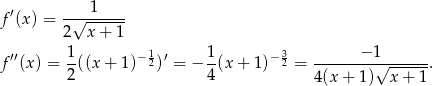
Ponieważ 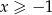 , druga pochodna jest stale niedodatnia, więc funkcja jest wklęsła.
, druga pochodna jest stale niedodatnia, więc funkcja jest wklęsła.
Na koniec obrazek.
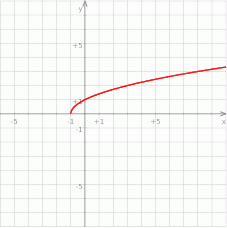
Odpowiedź: Wklęsła na całej dziedzinie.

