Zadanie nr 7206232
Wykaż, że podprzestrzeń 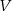 przestrzeni liniowej
przestrzeni liniowej 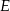 jest przestrzenią liniową (z działaniami takimi jak w
jest przestrzenią liniową (z działaniami takimi jak w 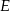 ).
).
Rozwiązanie
Najpierw musimy sprawdzić, czy działania dodawania wektorów i mnożenia przez skalar są dobrze określone w zbiorzez 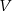 , tzn. czy nie wyprowadzają poza ten zbiór. To jednak jest dokładnie definicja podprzestrzeni liniowej.
, tzn. czy nie wyprowadzają poza ten zbiór. To jednak jest dokładnie definicja podprzestrzeni liniowej.
Co do własności tych działań, czyli aksjomatów przestrzeni liniowej, to nie musimy ich sprawdzać, bo są to te same działania, co działania w 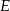 , więc mają żądane własności.
, więc mają żądane własności.

