Zadanie nr 7268129
Oblicz całkę 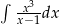 .
.
Rozwiązanie
Sposób I
Podstawiamy 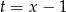 .
.
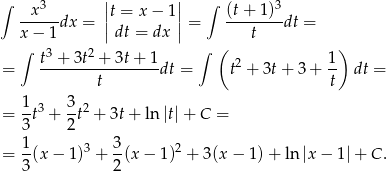
Sposób II
Dzielimy 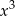 z resztą przez
z resztą przez 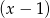 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
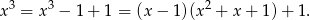
Mamy więc
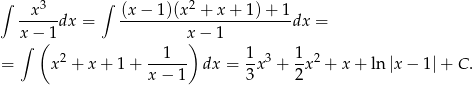
Odpowiedź: 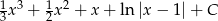
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 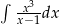 .
.
Sposób I
Podstawiamy 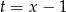 .
.
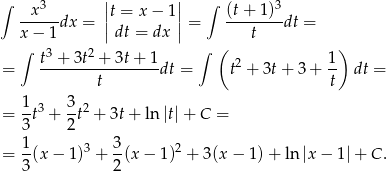
Sposób II
Dzielimy 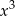 z resztą przez
z resztą przez 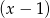 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
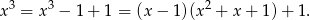
Mamy więc
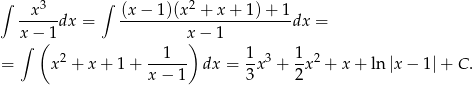
Odpowiedź: