Zadanie nr 7291202
Oblicz granicę 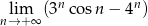 .
.
Rozwiązanie
Powinno być jasne, że dominujący składnik w tym wyrażeniu (ten który najszybciej rośnie) to 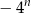 , więc granica powinna wyjść
, więc granica powinna wyjść 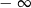 . Szacujemy
. Szacujemy
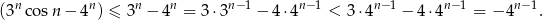
Ponieważ 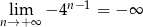 , więc taka sama jest granica danego ciągu (bo ma mniejsze wyrazy).
, więc taka sama jest granica danego ciągu (bo ma mniejsze wyrazy).
Odpowiedź: