Zadanie nr 7704179
Oblicz granicę 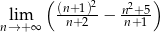 .
.
Rozwiązanie
Liczymy
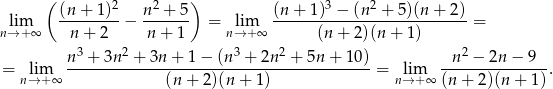
Dzielimy teraz licznik i mianownik przez 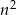 .
.
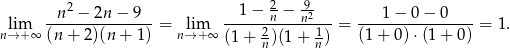
Odpowiedź: 1
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz granicę 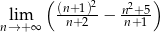 .
.
Liczymy
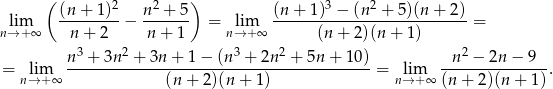
Dzielimy teraz licznik i mianownik przez 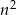 .
.
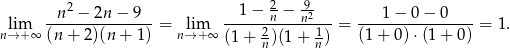
Odpowiedź: 1
