Zadanie nr 7730265
Oblicz pole obszaru ograniczonego parabolami 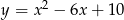 i
i 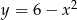 .
.
Rozwiązanie
Wyznaczmy punkty wspólne danych parabol.
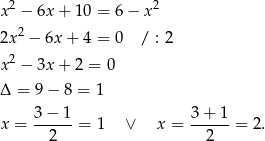
Szkicujemy teraz obrazek.
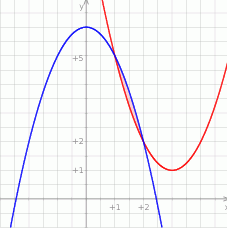
Z rysunku widać, że szukane pole jest równe
![∫ 2 ∫ 2 (6− x2 − (x2 − 6x + 10))dx = (− 2x2 + 6x − 4)dx = 1 1 [ 2 ]2 ( 16 ) ( 2 ) = − -x 3 + 3x 2 − 4x dx = − ---+ 12 − 8 − − --+ 3 − 4 = 3 1 3 3 14 1 = − 3--+ 5 = 3.](https://img.zadania.info/zad/7730265/HzadR2x.gif)
Odpowiedź: 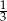
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz pole obszaru ograniczonego parabolami 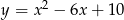 i
i 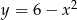 .
.
Wyznaczmy punkty wspólne danych parabol.
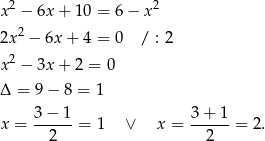
Szkicujemy teraz obrazek.

Z rysunku widać, że szukane pole jest równe
![∫ 2 ∫ 2 (6− x2 − (x2 − 6x + 10))dx = (− 2x2 + 6x − 4)dx = 1 1 [ 2 ]2 ( 16 ) ( 2 ) = − -x 3 + 3x 2 − 4x dx = − ---+ 12 − 8 − − --+ 3 − 4 = 3 1 3 3 14 1 = − 3--+ 5 = 3.](https://img.zadania.info/zad/7730265/HzadR2x.gif)
Odpowiedź: