Zadanie nr 7829265
Zbadać, czy ciąg 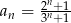 jest monotoniczny od pewnego miejsca.
jest monotoniczny od pewnego miejsca.
Rozwiązanie
Ponieważ 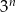 rośnie szybciej niż
rośnie szybciej niż 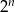 , więc należy oczekiwać, że ciąg jest malejący (inna wskazówka to, że jego granicą jest 0). Policzmy iloraz.
, więc należy oczekiwać, że ciąg jest malejący (inna wskazówka to, że jego granicą jest 0). Policzmy iloraz.
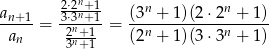
Chcemy uzasadnić, że jest on od pewnego miejsca mniejszy od 1. Spróbujemy rozwiązać nierówność 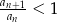
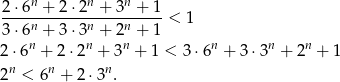
Nierówność ta jest oczywiście spełniona.
Odpowiedź: Ciąg jest malejący

