Zadanie nr 8273808
Oblicz wartość wyrażenia: 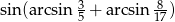 .
.
Rozwiązanie
Żeby trochę uprościć sobie zapis oznaczmy
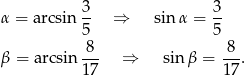
Skorzystamy ze wzoru na sinus sumy.
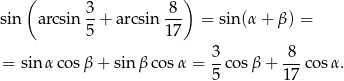
Aby móc dokończyć ten rachunek, musimy wyliczyć 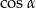 i
i 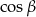 , łatwo to zrobić z jedynki trygonometrycznej (tu jest ważne, że
, łatwo to zrobić z jedynki trygonometrycznej (tu jest ważne, że  i
i 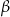 są kątami ostrymi – to wynika z definicji funkcji
są kątami ostrymi – to wynika z definicji funkcji 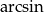 !)
!)
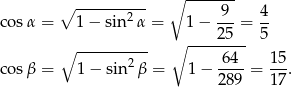
Zatem
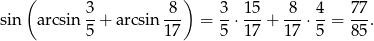
Odpowiedź: