Zadanie nr 8398267
Uzasadnij wzór
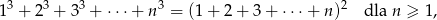
a następnie
- oblicz sumę sześcianów wszystkich liczb naturalnych dwucyfrowych;
- zapisz liczbę 14400 jako sumę sześcianów początkowych liczb naturalnych.
Rozwiązanie
Podany wzór uzasadnimy indukcyjnie. Zanim to jednak zrobimy, zauważmy, że na mocy wzoru na sumę ciągu arytmetycznego, możemy go zapisać w postaci
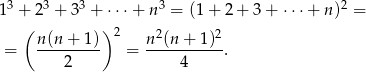
Dla 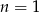 mamy oczywistą równość
mamy oczywistą równość
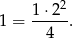
Załóżmy, że wzór zachodzi dla liczby naturalnej  i pokażemy jego prawdziwość dla liczby
i pokażemy jego prawdziwość dla liczby 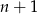 .
.
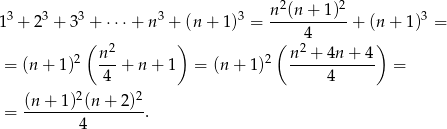
Jest to dokładnie prawa strona wzoru z podstawionym 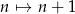 , co kończy dowód.
, co kończy dowód.
- Na podstawie udowodnionego wzoru, mamy
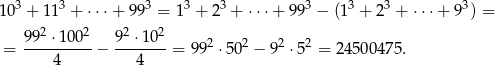
Odpowiedź: 24500475 - Musimy rozwiązać równanie
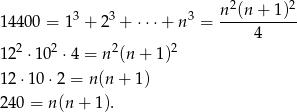
Można rozwiązać to równanie kwadratowe, ale łatwiej jest zgadnąć rozwiązanie:
 musi być bliskie
musi być bliskie 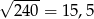 . Próbujemy więc
. Próbujemy więc 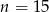 i wychodzi.
i wychodzi.
Odpowiedź: