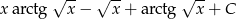Zadanie nr 8483221
Oblicz całkę 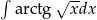 .
.
Rozwiązanie
Całkujemy przez części.
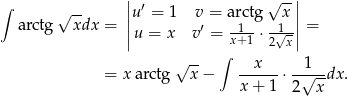
Ostatnią całkę obliczymy przez podstawienie 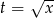 ,
,
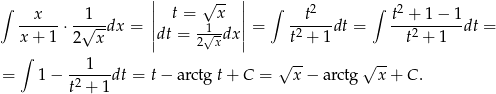
Zatem
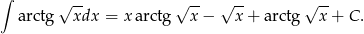
Odpowiedź: 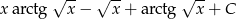
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz całkę 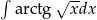 .
.
Całkujemy przez części.
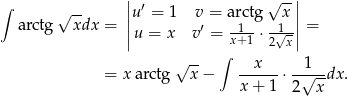
Ostatnią całkę obliczymy przez podstawienie 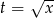 ,
,
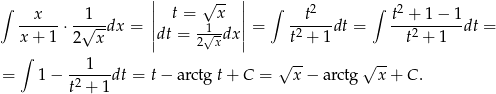
Zatem
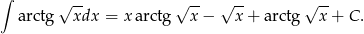
Odpowiedź: