Zadanie nr 9177559
Oblicz całkę 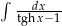 .
.
Rozwiązanie
Jeżeli podstawiamy 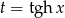 to
to
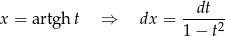
oraz
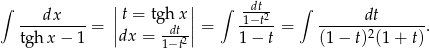
Ostatnią całkę liczymy szukając rozkładu na ułamki proste.
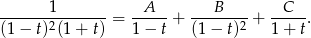
Mnożymy obie strony przez 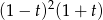 .
.
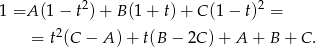
Daje to układ równań
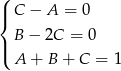
Podstawiając 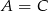 i
i 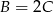 do ostatniego równania otrzymamy
do ostatniego równania otrzymamy 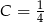 . Stąd
. Stąd 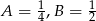 oraz
oraz
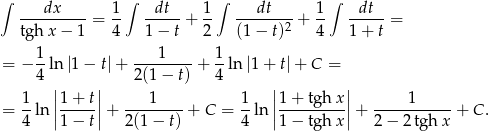
Odpowiedź: