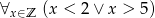Zadanie nr 9360339
Oceń wartość logiczną podanego zdania i napisz jego zaprzeczenie:
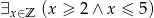
Rozwiązanie
Pisząc zaprzeczenia zdań będziemy korzystać z podstawowych praw rachunku zdań i kwantyfikatorów:
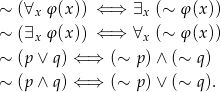
Zdanie jest prawdziwe, bo np. 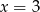 spełnia warunek pod kwantyfikatorem. Napiszmy teraz jego zaprzeczenie.
spełnia warunek pod kwantyfikatorem. Napiszmy teraz jego zaprzeczenie.
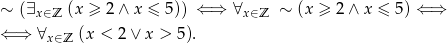
Odpowiedź: Prawdziwe. Zaprzeczenie: