Zadanie nr 9365874
Zbadaj monotoniczność ciągu 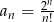 .
.
Rozwiązanie
Ponieważ wyrazy ciągu są dodatnie, wystarczy sprawdzić wartość ilorazu 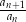
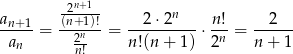
Zatem ciąg jest malejący dla 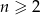 , czyli począwszy od drugiego wyrazu.
, czyli począwszy od drugiego wyrazu.
Odpowiedź: Malejący począwszy od drugiego wyrazu

