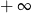Zadanie nr 9535794
Oblicz granicę ciągu 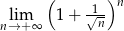 .
.
Rozwiązanie
Gdybyśmy mieli
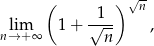
to granicą byłoby  . Mamy jednak w wykładniku
. Mamy jednak w wykładniku  , które zbiega do
, które zbiega do 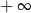 znacznie szybciej niż
znacznie szybciej niż 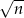 . Zatem powinno być jasne, że ciąg będzie rozbieżny do
. Zatem powinno być jasne, że ciąg będzie rozbieżny do 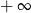 (bo
(bo 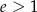 ).
).
Sposób I
Aby to porządnie uzasadnić, zapiszmy
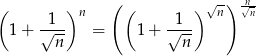
Jak już zauważyliśmy, ciąg w nawiasie zbiega do 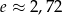 , zatem od pewnego miejsca jego wyrazy będą większe od 2. Mamy wtedy nierówność
, zatem od pewnego miejsca jego wyrazy będą większe od 2. Mamy wtedy nierówność
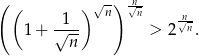
Prawa strona jest rozbieżna do 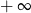 , więc lewa też.
, więc lewa też.
Sposób II
Korzystamy z nierówności Bernoulliego:
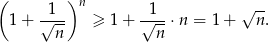
Ciąg otrzymany z prawej strony jest rozbieżny do 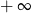 , więc ciąg z lewej strony też ma tę własność.
, więc ciąg z lewej strony też ma tę własność.
Odpowiedź: