Zadanie nr 9558208
Wykazać, że relacja izomorfizmu jest relacją równoważności w zbiorze przestrzeni liniowych.
Rozwiązanie
Musimy pokazać, że relacja ta jest zwrotna, symetryczna i przechodnia.
Zwrotność oznacza, że każda przestrzeń liniowa 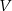 jest izomorficzna sama ze sobą. To jest jasne – izomorfizm to odwzorowanie
jest izomorficzna sama ze sobą. To jest jasne – izomorfizm to odwzorowanie 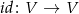 ,
, 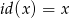 .
.
Symetryczność oznacza, że jeżeli przestrzeń 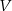 jest izomorficzna z
jest izomorficzna z 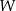 , to też
, to też 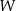 jest izomorficzne z
jest izomorficzne z 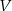 . Tak jest, bo jeżeli
. Tak jest, bo jeżeli 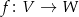 jest izomorfizmem to
jest izomorfizmem to 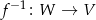 też jest izomorfizmem.
też jest izomorfizmem.
Przechodniość oznacza, że jeśli 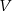 jest izomorficzna z
jest izomorficzna z 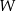 , a
, a 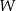 jest izomorficzna z
jest izomorficzna z 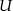 , to
, to 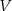 jest izomorficzna
jest izomorficzna 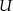 . Własność ta wynika z faktu, że złożenie
. Własność ta wynika z faktu, że złożenie 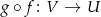 odwzorowań liniowych
odwzorowań liniowych 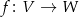 i
i 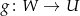 też jest izomorfizmem liniowym.
też jest izomorfizmem liniowym.

