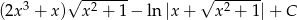Zadanie nr 9609387
Oblicz całkę 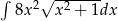 .
.
Rozwiązanie
Zastosujemy metodę współczynników nieoznaczonych, czyli fakt, że jeżeli 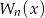 jest wielomianem stopnia
jest wielomianem stopnia  , to całka
, to całka
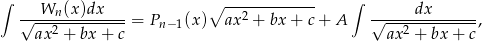
gdzie 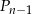 jest pewnym wielomianem stopnia
jest pewnym wielomianem stopnia 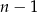 , a
, a 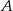 stałą.
stałą.
Ponieważ
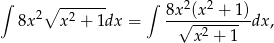
oczekujemy wyniku postaci
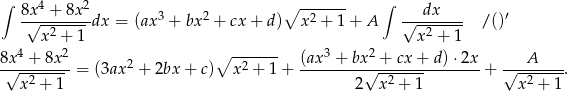
Mnożymy obie strony przez  i mamy
i mamy
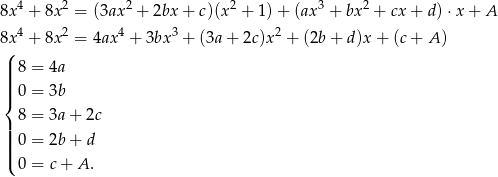
Łatwo stąd wyliczyć, że  . Zatem
. Zatem
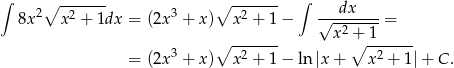
Odpowiedź: