Zadanie nr 9644615
Oblicz 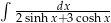 .
.
Rozwiązanie
Stosujemy podstawienie uniwersalne 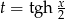 . Wtedy
. Wtedy
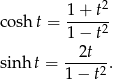
oraz
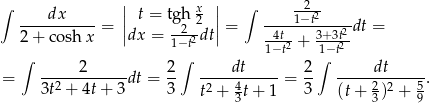
Teraz pozostało skorzystać ze wzoru
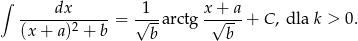
Mamy zatem
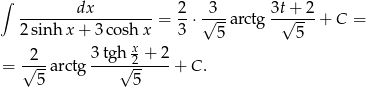
Odpowiedź: 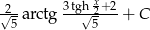
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz 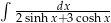 .
.
Stosujemy podstawienie uniwersalne 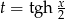 . Wtedy
. Wtedy
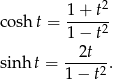
oraz
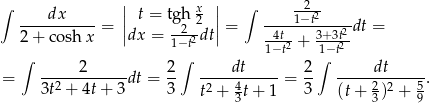
Teraz pozostało skorzystać ze wzoru
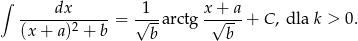
Mamy zatem
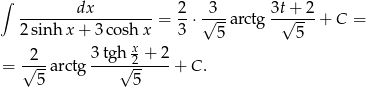
Odpowiedź: