Zadanie nr 9650521
Oblicz granicę 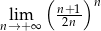 .
.
Rozwiązanie
Sposób I
Korzystamy z definicji liczby  .
.
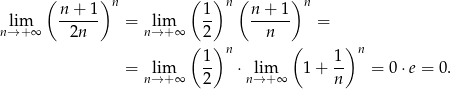
Sposób II
Ponieważ granica ciągu w nawiasie jest równa 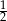 , więc ciąg będzie miał taką granicę jak ciąg
, więc ciąg będzie miał taką granicę jak ciąg  , czyli 0. Aby to porządnie uzasadnić, korzystamy z definicji granicy ciągu. Ponieważ
, czyli 0. Aby to porządnie uzasadnić, korzystamy z definicji granicy ciągu. Ponieważ 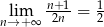 , więc dla dostatecznie dużych
, więc dla dostatecznie dużych  mamy
mamy 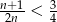 (szczerze mówiąc to nawet możemy rozwiązać tę nierówność i zobaczyć dla jakich
(szczerze mówiąc to nawet możemy rozwiązać tę nierówność i zobaczyć dla jakich  zachodzi). Mamy wtedy
zachodzi). Mamy wtedy
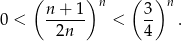
Ponieważ skrajne ciągi zbiegają do 0, więc taka sama musi być granica danego ciągu.
Odpowiedź: 0

