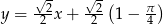Zadanie nr 9684958
Napisz równanie stycznej do wykresu funkcji 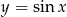 w punkcie
w punkcie 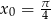 .
.
Rozwiązanie
Korzystamy z równania stycznej do wykresu funkcji 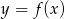 w punkcie
w punkcie 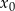
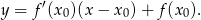
Liczymy
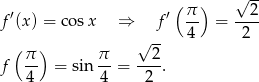
Zatem styczna ma równanie
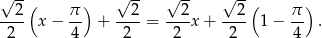
Na koniec obrazek
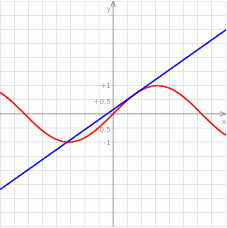
Odpowiedź: 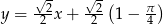
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Napisz równanie stycznej do wykresu funkcji 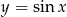 w punkcie
w punkcie 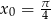 .
.
Korzystamy z równania stycznej do wykresu funkcji 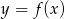 w punkcie
w punkcie 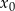
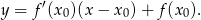
Liczymy
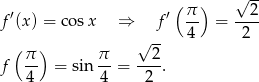
Zatem styczna ma równanie
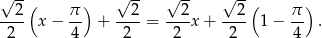
Na koniec obrazek

Odpowiedź: