Zadanie nr 1500599
Funkcja 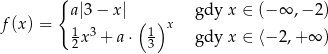 jest ciągła w zbiorze liczb rzeczywistych jeżeli
jest ciągła w zbiorze liczb rzeczywistych jeżeli  jest równe
jest równe
A) 1 B) 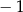 C)
C) 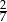 D)
D) 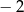
Rozwiązanie
Jeżeli funkcja 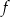 ma być ciągła w punkcie
ma być ciągła w punkcie 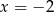 , to obydwa wzory definiujące
, to obydwa wzory definiujące 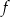 w otoczeniu
w otoczeniu 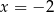 muszą dawać tę samą wartość. Tak będzie, gdy
muszą dawać tę samą wartość. Tak będzie, gdy
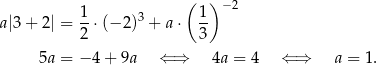
Na koniec wykres funkcji dla ciekawskich.
Odpowiedź: A

