Zadanie nr 6004264
Wartość wyrażenia 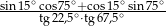 jest równa
jest równa
A) 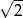 B)
B) 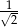 C) 1 D)
C) 1 D) 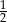
Rozwiązanie
Korzystamy ze wzorków
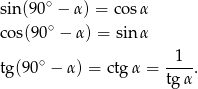
Liczymy
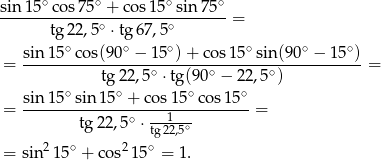
Licznik mogliśmy też obliczyć korzystając ze wzoru
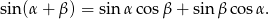
Odpowiedź: C
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wartość wyrażenia 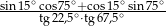 jest równa
jest równa
A) 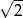 B)
B) 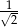 C) 1 D)
C) 1 D) 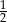
Korzystamy ze wzorków
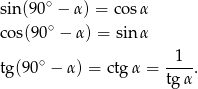
Liczymy
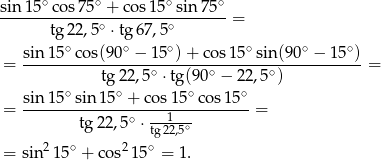
Licznik mogliśmy też obliczyć korzystając ze wzoru
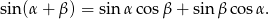
Odpowiedź: C
