/Szkoła podstawowa/Geometria/Figury przestrzenne

Zadanie nr 2702927

Dodaj do ulubionych
Dodaj do rozwiązanych

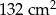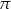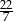Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej figury ma długość 33 cm, a jej pole jest równe 13 2 cm 2 . Oblicz objętość tego pudełka. Przyjmij przybliżenie π równe 272 . Zapisz obliczenia.

PIC

Rozwiązanie

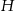Oznaczmy promień podstawy walca przez r , a jego wysokość przez H . Długość dłuższego boku równoległoboku to dokładnie długość okręgu w podstawie walca, czyli

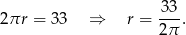
2πr = 33 ⇒ r = 33-. 2π

Wysokość walca jest równa wysokości równoległobku, więc możemy ją obliczyć z podanego pola równoległoboku.

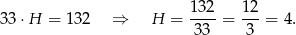
33⋅ H = 132 ⇒ H = 132-= 12-= 4 . 33 3

Objętość walca jest więc równa

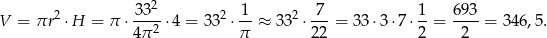
2 V = πr2 ⋅H = π ⋅ 3-3-⋅4 = 332⋅ 1-≈ 332⋅-7- = 33 ⋅3⋅7 ⋅ 1-= 693-= 346,5. 4π 2 π 2 2 2 2

 
Odpowiedź: 3 346 ,5 cm

Wersja PDF