/Szkoła podstawowa/Geometria/Figury przestrzenne

Zadanie nr 3869231

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.

Rozwiązanie

Niech a będzie długością krawędzi podstawy, a 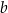b długością krawędzi bocznej graniastosłupa.

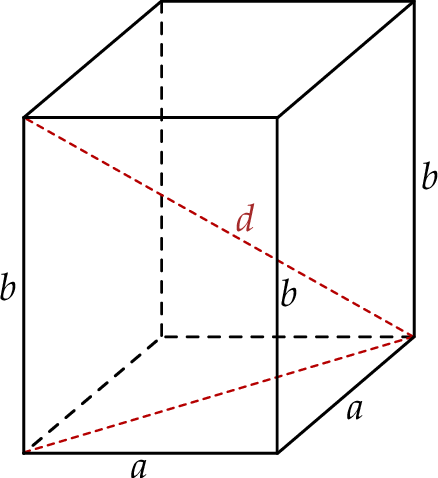
ZINFO-FIGURE

Z podanych informacji mamy zatem

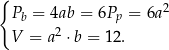
{ Pb = 4ab = 6Pp = 6a 2 2 V = a ⋅b = 12.

Z pierwszego równania mamy 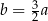3 b = 2a . Wstawiamy to wyrażenie do drugiego równania.

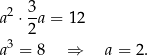
2 3- a ⋅ 2a = 12 3 a = 8 ⇒ a = 2.

Stąd 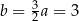3 b = 2a = 3 .

Długość przekątnej graniastosłupa obliczamy korzystając z twierdzenia Pitagorasa.

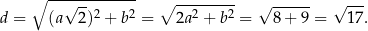
∘ --√---------- ∘ --------- √ ------ √ --- d = (a 2 )2 + b2 = 2a2 + b2 = 8 + 9 = 1 7.

 
Odpowiedź: Krawędź podstawy: 2, przekątna: 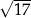√ --- 17 .

Wersja PDF